
Back Модел на Хъбърд Bulgarian Model de Hubbard Catalan Hubbard-Modell German Modelo de Hubbard Spanish Modèle de Hubbard French מודל האברד HE Modello di Hubbard Italian ハバード模型 Japanese Model Hubbarda Polish Modelo de Hubbard Portuguese
The Hubbard model is an approximate model used to describe the transition between conducting and insulating systems.[1] It is particularly useful in solid-state physics. The model is named for John Hubbard.
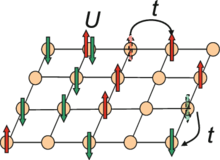
The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors.[2] Its Hamiltonian thus has two terms: a kinetic term allowing for tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model".
The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed to be in the lowest Bloch band, and long-range interactions between the particles can be ignored. If interactions between particles at different sites of the lattice are included, the model is often referred to as the "extended Hubbard model". In particular, the Hubbard term, most commonly denoted by U, is applied in first principles based simulations using Density Functional Theory, DFT. The inclusion of the Hubbard term in DFT simulations is important as this improves the prediction of electron localisation and thus it prevents the incorrect prediction of metallic conduction in insulating systems.[3]
The Hubbard model introduces short-range interactions between electrons to the tight-binding model, which only includes kinetic energy (a "hopping" term) and interactions with the atoms of the lattice (an "atomic" potential). When the interaction between electrons is strong, the behavior of the Hubbard model can be qualitatively different from a tight-binding model. For example, the Hubbard model correctly predicts the existence of Mott insulators: materials that are insulating due to the strong repulsion between electrons, even though they satisfy the usual criteria for conductors, such as having an odd number of electrons per unit cell.
- ^ Altland, A.; Simons, B. (2006). "Interaction effects in the tight-binding system". Condensed Matter Field Theory. Cambridge University Press. pp. 58 ff. ISBN 978-0-521-84508-3.
- ^ Cite error: The named reference
:0was invoked but never defined (see the help page). - ^ Fronzi, Marco; Assadi, M. Hussein N.; Hanaor, Dorian A.H. (2019). "Theoretical insights into the hydrophobicity of low index CeO2 surfaces". Applied Surface Science. 478: 68–74. arXiv:1902.02662. Bibcode:2019ApSS..478...68F. doi:10.1016/j.apsusc.2019.01.208. S2CID 118895100.