Regular icosahedron

Regular icosahedron
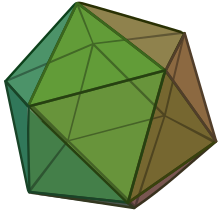Type	Gyroelongated bipyramid Deltahedron
Faces	20
Edges	30
Vertices	12
Vertex configuration	${\displaystyle 12\times \left(3^{5}\right)}$
Symmetry group	Icosahedral symmetry ${\displaystyle I_{h}}$
Dihedral angle (degrees)	138.190 (approximately)
Dual polyhedron	Regular dodecahedron
Properties	convex, composite
Net

In geometry, the regular icosahedron (or simply icosahedron) is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with regular faces to each of its pentagonal faces, or by putting points onto the cube. The resulting polyhedron has 20 equilateral triangles as its faces, 30 edges, and 12 vertices. It is an example of a Platonic solid and of a deltahedron. The icosahedral graph represents the skeleton of a regular icosahedron.

Many polyhedrons are constructed from the regular icosahedron. For example, most of the Kepler–Poinsot polyhedron is constructed by faceting. Some of the Johnson solids can be constructed by removing the pentagonal pyramids. The regular icosahedron has many relations with other Platonic solids, one of them is the regular dodecahedron as its dual polyhedron and has the historical background on the comparison mensuration. It also has many relations with other polytopes.

The appearance of regular icosahedron can be found in nature, such as the virus with icosahedral-shaped shells and radiolarians. Other applications of the regular icosahedron are the usage of its net in cartography, twenty-sided dice that may have been found in ancient times and role-playing games.